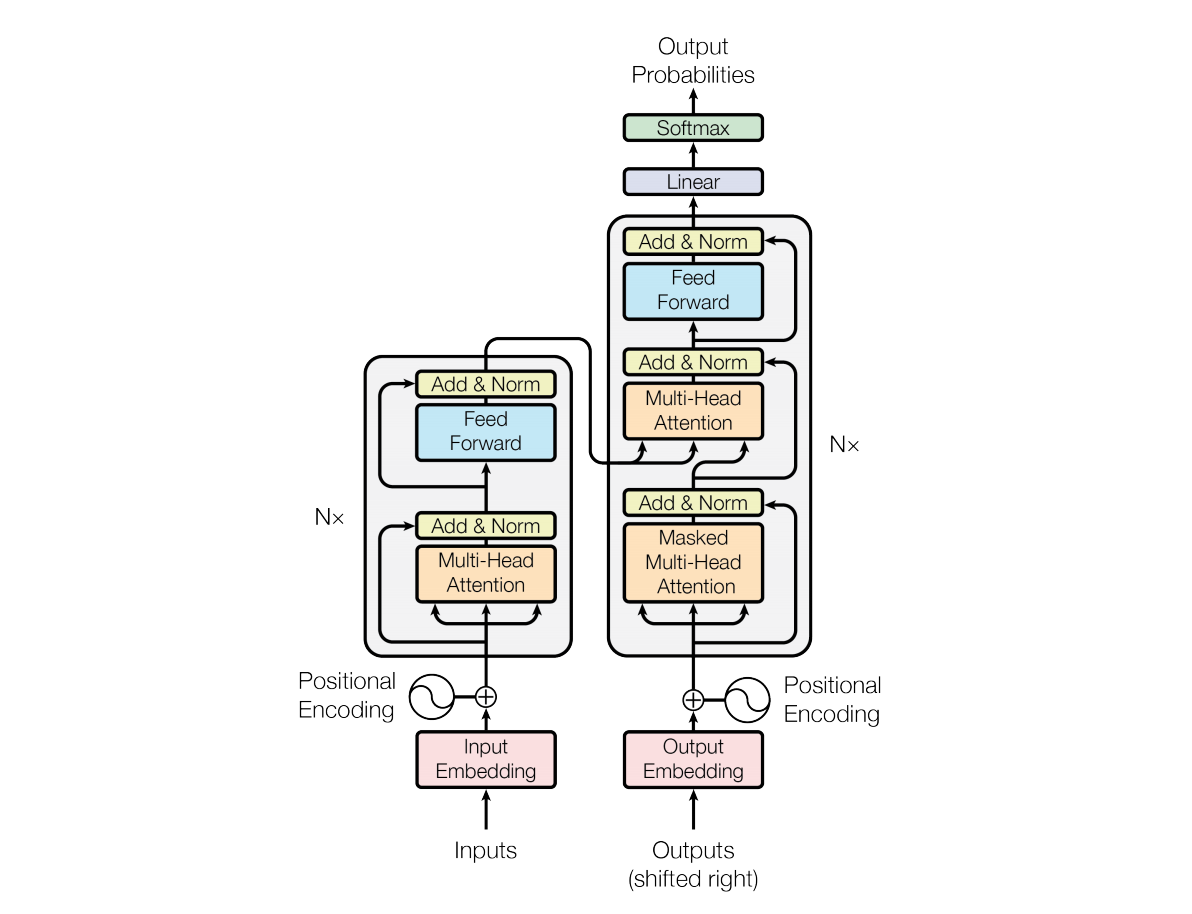
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
| import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import math
import matplotlib.pyplot as plt
import numpy as np
import copy
embedding = nn.Embedding(10,3)
input1 = torch.LongTensor([[1,2,4,5],[4,3,2,9]])
print(embedding(input1))
embedding = nn.Embedding(10, 3, padding_idx=0)
input1 = torch.LongTensor([[0, 2, 0, 5]])
print(embedding(input1))
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
d_model = 512
vocab = 1000
x = Variable(torch.LongTensor([[100, 2, 421, 508], [491, 998, 1, 221]]))
emb = Embeddings(d_model, vocab)
embr = emb(x)
print("ember:", embr)
print(embr.shape)
m = nn.Dropout(p=0.2)
input1 = torch.randn(4, 5)
output = m(input1)
print(output)
x = torch.tensor([1, 2, 3, 4])
y = torch.unsqueeze(x, 0)
print(y)
z = torch.unsqueeze(x, 1)
print(z)
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0)))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
return self.dropout(x)
d_model = 512
dropout = 0.1
max_len = 60
x = embr
pe = PositionalEncoding(d_model, dropout, max_len)
pe_result = pe(x)
print(pe_result)
plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)
y = pe(Variable(torch.zeros(1, 100, 20)))
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
plt.legend(["dim %d"%p for p in [4, 5, 6, 7]])
plt.show()
|